project07:W1
Ori Gilboa
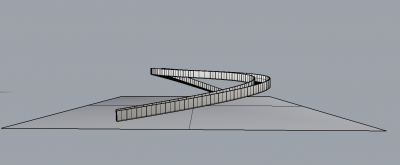
In my project I tried to develop a curved walk-able 3D path. At first, it sounds as an easy assignment to achieve. I was a bit surprised that for the right orientation of the surface and the railing it proved to be a mathematical challenge that required some thinking, as there is no specific tool in grasshopper that I could use.
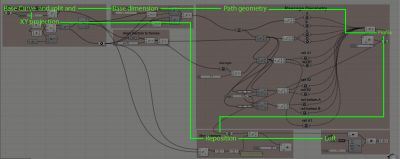
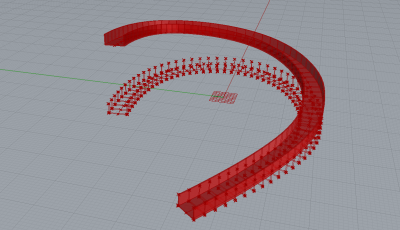
At first I tried to use the command of create perpendicular frames – the result is a series of perpendicular frames to a 3D curve. Unfortunately, in this situation there is no way to orient up and down – which is essential for paths and railings. The result is more like a rollercoaster path rather than a walkable one. For this reason I rethought about how to generate it in a thorough way. Base Geometry: The path required a 3D curve. The curve splits into equal segments – and each is being assign with the railing profile – with changeable width and height. In the end – the loft and cap command makes it into a 3D object.
Orientation: In order to make the path walkable each part supposed to be horizontal to the ground plane. For that – the curve is projected into the XY plane. Afterwards, the XY curve is split and a profile is generated in each segment. This creates a horizontal path – but for a 3D curving and climbing-up path this won’t do. The next step is that every segment is moved-up into its appropriate point in the original curve. Only then the loft command is applied.